First of all, I would like to thank the volunteers of the SIAM chapter for organizing these weekly math graduate colloquia. Since my first semester here, at Tulane, I have been putting in an appearance every semester in these talks, both as a speaker and an audience. Be it my research findings or something I find intriguing, I always try to bring it along in the colloquium. With the talk today, I conclude the continuity as I am graduating this semester. It always has been a place to learn something new from my peers. Moreover, it's a great place to mingle with the fellow students, know about their research projects, eat pizza. I am not an extempore speaker. This platform has given me the opportunity to practice my talks and presentations and receive feedback. The talks here have undoubtedly helped me to express myself more eloquently. I hope the future students will continue to keep up the tradition.
Without further adieu, let me start.
Today, I will walk you through the regime of Shape Reconstruction and introduce a few related notions, like Hausdorff and Gromov-Hausdorff distance.
For this talk, I am using a new technology. The idea is we can get a (client) copy of the presentation on your device by either scanning the QR code or by hitting this url using your browser. Then, you can follow along as I move through the slides.

Shape Comparison and Gromov-Hausdorff Distance

Sushovan "Sush" MAJHI

Tulane University (January 21, 2020)

Scan the above QR or hit the following url: smajhi.com/gh-presentation

The Manifesto

Introduction to Shape Comparison
Hausdorff Distance
Gromov-Hausdorff Distance
Computing the Gromov-Hausdorff Distance
Questions, Discussions, and 🍕 Pizza.

Collaborators

Carola Wenk
Computer Science, Tulane

Jeffrey Vitter
Computer and Information Science, University of Mississippi

Motivation

1. Distinguish Shapes

circle

triangle

2. Classify Shapes

triangular

circular

3. Quality Guarantee

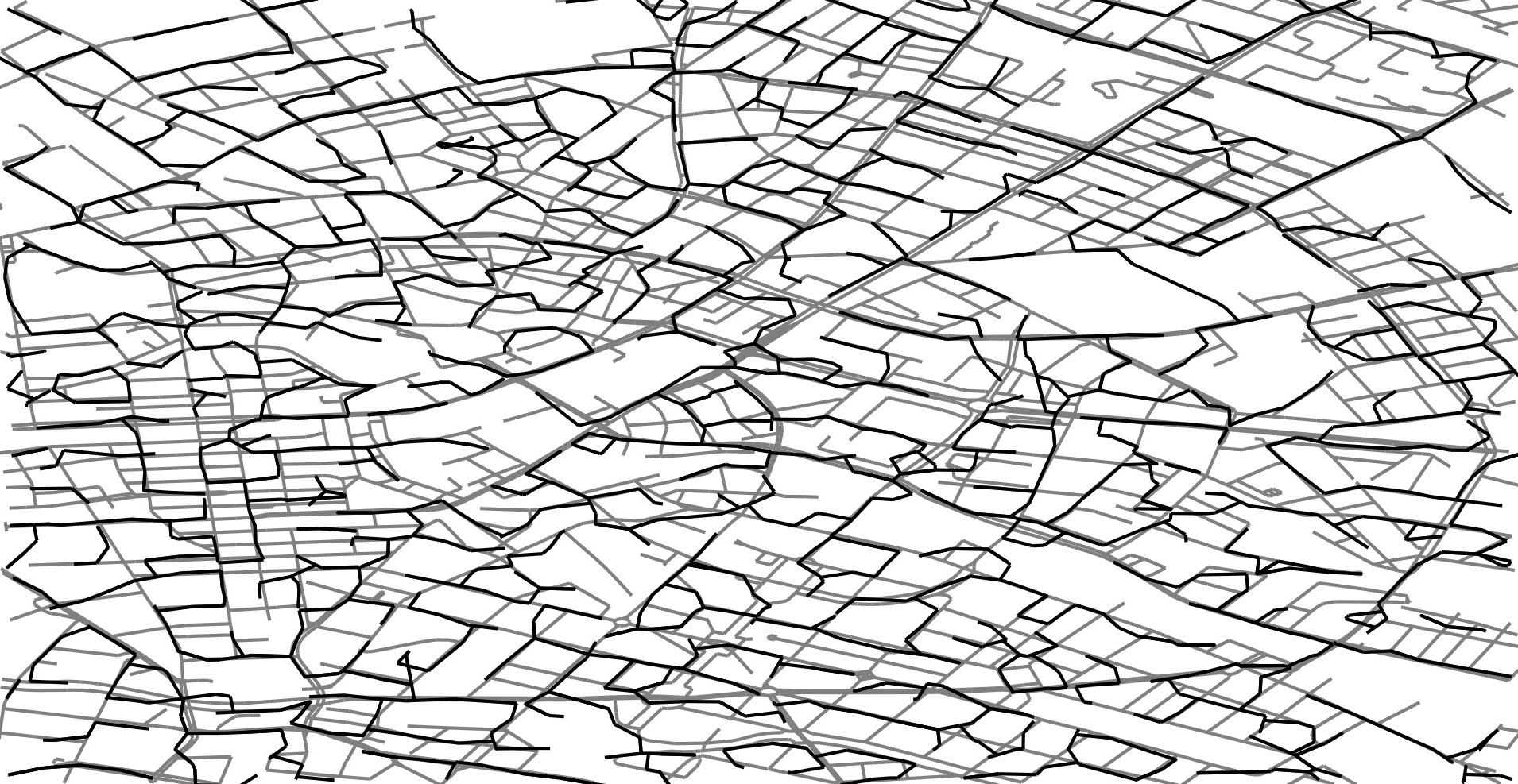
Map Construction from GPS data (Berlin)
https://mapconstruction.org

Shape Comparison

A shape can be modeled as a metric space $(X,d_X)$.

We need an appropriate notion of a distance measure $d_?(X,Y)$ so that

$d_?(X,Y)$ defines a pseudo-metric on the class of metric spaces.

$d_?(X,Y)$ large $\iff$ very different shape

$d_?(X,Y)$ small $\iff$ $X=Y$ up to a class of deformation.

Hausdorff Distance

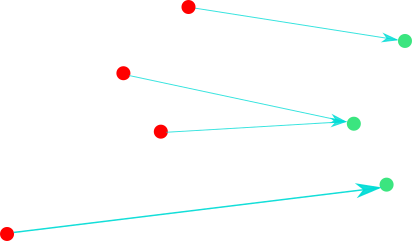
Nearest neighbor distance (red points $\to$ green points).

Let $A,B\subseteq\mathbb{R}^N$. The directed Hausdorff distance from $A$ to $B$ is defined by $$\overrightarrow{d}_H(A,B)=\sup_{a\in A}\inf_{b\in B}\|a-b\|.$$

For any two compact $X,Y\subset\mathbb{R}^N$, $$d_H(X,Y)=\max\left\{\overrightarrow{d}_H(X,Y),\overrightarrow{d}_H(Y,X)\right\}$$
For any two compact $X,Y\subset(Z,d_Z)$, $$d^Z_H(X,Y)=\max\left\{\overrightarrow{d}^Z_H(X,Y),\overrightarrow{d}^Z_H(Y,X)\right\}$$

$d^Z_H(X,Y)\geq0$,

$d^Z_H(X,Y)=d^Z_H(Y,X)$,

$d^Z_H(X,Y)=0\iff X=Y$, and

$d^Z_H(A,C)\leq d^Z_H(A,B)+d^Z_H(B,C)$.

The Hausdorff distance induces a complete metric space on the set of all compact subsets of a metric space.

💡

$d_H$ is sensitive to Shape + Size + Placement.

Hausdorff under Isometry

$d_H($◤, ◢ $)=$ large.

Let $\mathcal{E}(N)$ denote the class of Euclidean isometries or distance preserving maps $T:\mathbb{R}^N\to\mathbb{R}^N$ i.e. $\|T(a)-T(b)\|=\|a-b\|$.

For $N=1$, $T$ is translation or reflection.

For $N=2$, $T$ is rotation, translation or reflection.

For $X,Y\subseteq\mathbb{R}^N$, we define $$d_{H,iso}(X,Y)=\inf\limits_{T\in\mathcal{E}(N)}d_H\left(X,T(Y)\right)$$

💡

$d_{H,iso}$ is sensitive to Shape + Size + ~~Placement~~.
$d_{H,iso}($◤, ◢ $)=0$.

Gromov-Hausdorff Distance

How to compare shapes that do not have a common embedding?

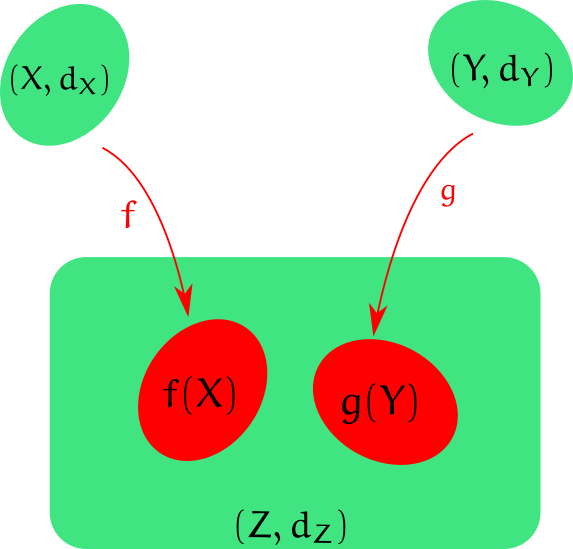
Isometric Embedding

For two abstract metric spaces $(X,d_X)$ and $(Y,d_Y)$, we define $$d_{GH}(X,Y)=\inf\limits_{f,g,Z} d^Z_H(f(X),g(Y)).$$

$d_{GH}$ vs $d_{H,iso}$

Let $X,Y\subseteq(\mathbb{R}^N,\|\cdot\|)$ be compact. Then, both $d_{GH}(X,Y)$ and $d_{H,iso}(X,Y)$ are defined. $$d_{GH}(X,Y)\leq d_{H,iso}(X,Y)\leq c_N\sqrt{Md_{GH}(X,Y)},$$ where $M=\max\{diam(X),diam(Y)\}$.

For $X,Y\subseteq\mathbb{R}^1$, we have $$d_{GH}(X,Y)\leq d_{H,iso}(X,Y)\leq\left(1+\frac{1}{4}\right)d_{GH}(X,Y),$$ and the upper bound is tight.

Computing $d_{GH}$

For $|X|,|Y|\leq k$, computing $d_{GH}(X,Y)$ takes $O(2^k)$ time.
For $X,Y\subset\mathbb{R}^1$ and $|X|,|Y|\leq k$, computing $d_{H,iso}(X,Y)$ takes $O(k\log{k})$ time.

Sometimes, computing the exact optimal solution ($s_{opt}$) to an optimization problem is HARD.

💡

Computing an approximate solution ($s_{appx}$) is sometimes more efficient.

For $\rho>1$, if we have $$s_{opt}\leq s_{appx}\leq\rho s_{opt},$$ then the algorithm is called an approximation algorithm with an approximation factor $\rho$ .

$$d_{GH}(X,Y)\leq d_{H,iso}(X,Y)\leq\left(1+\frac{1}{4}\right)d_{GH}(X,Y),$$

💡

$d_{H,iso}$ approximates $d_{GH}$ with an approximate factor of $\left(1+\frac{1}{4}\right)$.

This Presentation

The framework is called RevealJS
Language: JavaScript
Platform: (modern) Web Browsers
Latex Support: MathJax
Features: Multiplexing, Notes, Timer, Autoslide, and more.

The speaker will now accept
QUESTIONS.